对于公交车悖论的一些代码研究

主要是12月要做个班会，心血来潮搞了一些代码，觉得也挺有意思的，可能以后班会的时候也会放给同学看。本人就会一点C++，所以Python代码都是豆包写的。

这篇文章纯是被毕导启发，大家快去关注他。如果看不懂我在干嘛，一定要去看毕导的视频！不要举办我😭😭

【注】（大佬请忽略，新手爱记录）对于所有Python代码，请先确保安装Python本体和numpy、matplotlib以及spicy库。若还没有安装，请先在Welcome to Python.org安装Python，安装后在控制台中输入：

pip install numpy matplotlib scipy

对于C++代码，请先确保安装C++。若未安装，请先前往Dev-C++ download | SourceForge.net安装C++。

当然，如果你有其他编译器等，可以使用你自己的。

1.对于特殊情况的研究

对于一个小时内到站6辆公交车，且第6辆公交车严格在第60分钟时到站的情况下，定义公交车司机的“精准度”\(x\)。“精准度”就是指这个公交车司机与上一位公交车司机的时间间隔在\((10-x)\)分钟到\((10+x)\)之间。

接下来这段代码绘制了折线图，横轴为“精准度”\(x\)，纵轴为乘客平均等待时间：

import numpy as np
import matplotlib.pyplot as plt
import time

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

def calculate_avg_wait(x, num_simulations=100000):
    """
    计算精准度x下的平均等待时间（第六辆公交车严格在60分钟到站）
    约束：共6辆公交车，间隔i1~i6∈[10-x,10+x]，且i1+i2+i3+i4+i5+i6=60
    """
    a = 10 - x  # 间隔最小值
    b = 10 + x  # 间隔最大值
    sum_sq_list = []  # 存储每次模拟的间隔平方和
    
    for _ in range(num_simulations):
        # 生成满足约束的6个间隔（通过u变量转换）
        while True:
            # 生成前5个u变量（u1~u5∈[0,1]）
            u = np.random.uniform(0, 1, size=5)
            sum_u = np.sum(u)
            u6 = 3 - sum_u  # 第6个u变量（因sum(u1~u6)=3）
            # 检查u6是否在[0,1]（确保所有u∈[0,1]）
            if 0 <= u6 <= 1:
                break  # 满足条件则退出循环
        
        # 计算6个间隔（i_j = a + 2x*u_j，因b-a=2x）
        u = np.append(u, u6)  # 拼接u1~u6
        intervals = a + 2 * x * u
        
        # 计算间隔平方和（用于后续平均等待时间计算）
        sum_sq = np.sum(intervals **2)
        sum_sq_list.append(sum_sq)
    
    # 平均等待时间 = 平方和的平均值 / 120（推导同前）
    avg_wait = np.mean(sum_sq_list) / 120.0
    return avg_wait

# 精准度x范围：0.0到9.9，步长0.1
x_values = np.arange(0.0, 10.0, 0.1)
avg_wait_results = []

start_time = time.time()

# 遍历所有x值计算平均等待时间
for idx, x in enumerate(x_values):
    avg_wait = calculate_avg_wait(x, num_simulations=100000)
    avg_wait_results.append(avg_wait)
    
    # 打印进度（含耗时预估）
    if (idx + 1) % 10 == 0 or idx == len(x_values) - 1:
        elapsed = time.time() - start_time
        remaining = elapsed * (len(x_values) - idx - 1) / (idx + 1)
        print(f"已完成 {idx + 1}/100 个x值（x={x:.1f}），平均等待时间：{avg_wait:.4f}分钟 | "
              f"已耗时：{elapsed:.1f}秒，预计剩余：{remaining:.1f}秒")

# 绘制折线图
plt.figure(figsize=(12, 6))
plt.plot(x_values, avg_wait_results, color='darkblue', linewidth=2)
plt.scatter(x_values, avg_wait_results, color='darkblue', s=15, alpha=0.7)
plt.xlabel('公交车司机精准度x', fontsize=12)
plt.ylabel('乘客平均等待时间（分钟）', fontsize=12)
plt.title('公交车精准度与平均等待时间的关系（第六辆严格60分钟到站，100000次模拟/每x值）', fontsize=14)
plt.grid(True, linestyle='--', alpha=0.6)
plt.xlim(0, 9.9)
plt.ylim(min(avg_wait_results)*0.95, max(avg_wait_results)*1.05)
plt.text(0.5, max(avg_wait_results)*0.98, "约束：6辆公交车，间隔∈[10-x,10+x]，总和=60分钟", 
         fontsize=10, color='gray')
plt.show()

运行时间大概为2-3分钟（在我的PC上），运行结果如下：

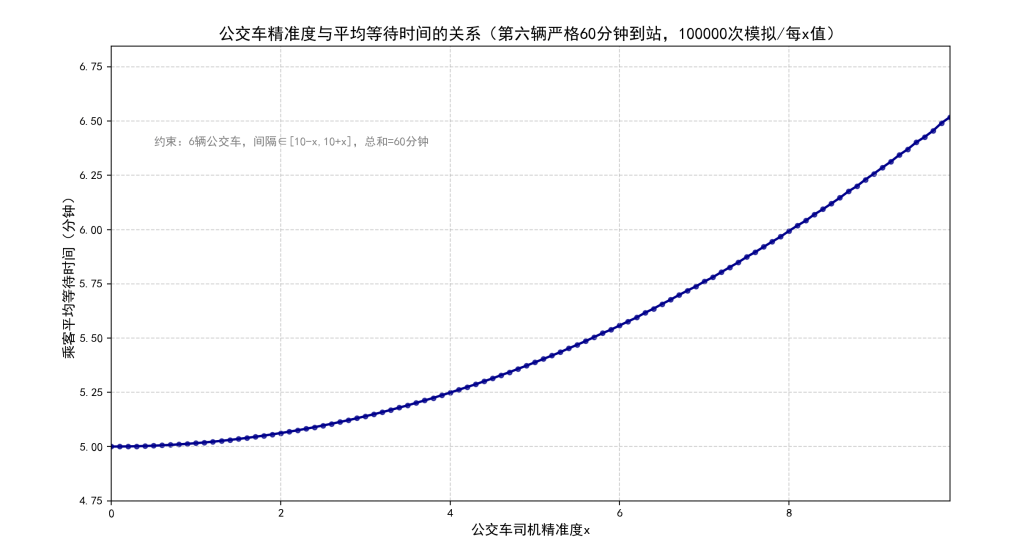
可以观察到，随着\(x\)的增大，乘客的等待时间单调递增。

2.对于日常情况的研究

对于任意时间间隔到站的6辆公交车（不强制要求严格在第60分钟到站），我们计算乘客在这6辆公交车到站间隔间的平均等待时间。对于到站时间间隔，2辆公交车间的间隔符合正态分布。

接下来这段代码绘制了柱状图，横轴为平均时间间隔，竖轴为1000000计算次数中乘客的平均等待时间的区间的占比：

import numpy as np
import matplotlib.pyplot as plt
import time

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

# ----------------------
# 1. 设计到站间隔概率分布（标准差=5，0-3分钟总概率≈5%，对称分布）
# ----------------------
# 时间区间：每1分钟一个，共20个（0-1,1-2,...,19-20分钟）
intervals = [(i, i+1) for i in range(20)]

# 手动设计对称概率（确保0-3分钟总概率≈5%，17-20分钟对称，中间高）
# 0-10分钟与10-20分钟严格对称（索引i与19-i概率相同）
probabilities = np.array([
    0.012,  # 0-1分钟
    0.015,  # 1-2分钟
    0.023,  # 2-3分钟（0-3分钟总：0.012+0.015+0.023=0.05=5%）
    0.030,  # 3-4分钟
    0.040,  # 4-5分钟
    0.055,  # 5-6分钟
    0.070,  # 6-7分钟
    0.080,  # 7-8分钟
    0.085,  # 8-9分钟
    0.088,  # 9-10分钟
    0.088,  # 10-11分钟（与9-10对称）
    0.085,  # 11-12分钟（与8-9对称）
    0.080,  # 12-13分钟（与7-8对称）
    0.070,  # 13-14分钟（与6-7对称）
    0.055,  # 14-15分钟（与5-6对称）
    0.040,  # 15-16分钟（与4-5对称）
    0.030,  # 16-17分钟（与3-4对称）
    0.023,  # 17-18分钟（与2-3对称）
    0.015,  # 18-19分钟（与1-2对称）
    0.012   # 19-20分钟（与0-1对称，17-20总：0.023+0.015+0.012=0.05=5%）
])

# 归一化（确保总和为1，修正手动输入的微小误差）
probabilities = probabilities / np.sum(probabilities)

# 验证关键指标
print("0-3分钟总概率：", probabilities[:3].sum().round(4))  # 应≈0.05
print("17-20分钟总概率：", probabilities[17:].sum().round(4))  # 应≈0.05
print("前10区间与后10区间对称性验证：", np.allclose(probabilities[:10], probabilities[10:][::-1]))  # 应True
assert np.isclose(sum(probabilities), 1.0), "概率总和必须为1.0"


# ----------------------
# 2. 生成随机到站间隔（批量处理）
# ----------------------
def generate_intervals(num_groups=1000000, buses_per_group=6):
    """生成100万组，每组6辆公交车的到站间隔"""
    total_samples = num_groups * buses_per_group  # 600万样本
    # 按概率分布选择区间索引
    interval_indices = np.random.choice(
        len(intervals),
        size=total_samples,
        p=probabilities
    )
    # 在区间内均匀生成具体时间
    starts = np.array([intervals[i][0] for i in interval_indices])
    ends = np.array([intervals[i][1] for i in interval_indices])
    intervals_random = starts + np.random.random(total_samples) * (ends - starts)
    return intervals_random.reshape(num_groups, buses_per_group)


# ----------------------
# 3. 计算平均等待时间
# ----------------------
def calculate_avg_wait_times(intervals_matrix):
    """平均等待时间公式：sum(间隔²) / (2 × 总间隔时间)"""
    sum_sq = np.sum(intervals_matrix **2, axis=1)
    sum_total = np.sum(intervals_matrix, axis=1)
    sum_total = np.maximum(sum_total, 1e-6)  # 避免除0
    return sum_sq / (2 * sum_total)


# ----------------------
# 4. 主程序：模拟并绘图
# ----------------------
if __name__ == "__main__":
    start_time = time.time()
    num_groups = 1000000  # 100万组模拟
    
    # 生成到站间隔
    print("\n生成100万组公交车到站间隔...")
    intervals_matrix = generate_intervals(num_groups=num_groups)
    print(f"生成完成，耗时：{time.time() - start_time:.2f}秒")
    
    # 计算平均等待时间
    print("计算平均等待时间...")
    avg_wait_times = calculate_avg_wait_times(intervals_matrix)
    print(f"计算完成，耗时：{time.time() - start_time:.2f}秒")
    
    # 过滤极端值（聚焦0-20分钟，覆盖>99.9%的数据）
    avg_wait_times = avg_wait_times[(avg_wait_times >= 0) & (avg_wait_times <= 20)]
    
    # 绘制柱状图（0.5分钟分度值，带间隔）
    print("绘制柱状图...")
    plt.figure(figsize=(14, 6))
    bin_width = 0.5  # 分度值0.5分钟
    bins = np.arange(0, 20.1, bin_width)
    
    # 绘制直方图（rwidth=0.8留间隔）
    n, bins, patches = plt.hist(
        avg_wait_times,
        bins=bins,
        density=True,
        alpha=0.7,
        color='forestgreen',
        rwidth=0.8
    )
    
    # 图表装饰
    plt.xlabel('平均等待时间（分钟）', fontsize=12)
    plt.ylabel('在100万组中的占比', fontsize=12)
    plt.title('6辆公交车平均等待时间分布（标准差=5，0.5分钟分度值）', fontsize=14)
    plt.grid(axis='y', linestyle='--', alpha=0.6)
    plt.xticks(np.arange(0, 20.1, 1))  # 每1分钟标刻度
    plt.text(12, max(n)*0.9, "到站间隔：0-3分钟总概率≈5%，对称分布，标准差=5", 
             fontsize=10, color='gray')
    plt.show()
    
    print(f"总耗时：{time.time() - start_time:.2f}秒")

这段代码运行时间远短于上一条（可能是上一条既要求了严格第60分钟到站，测试次数也非常多），运行结果如下：

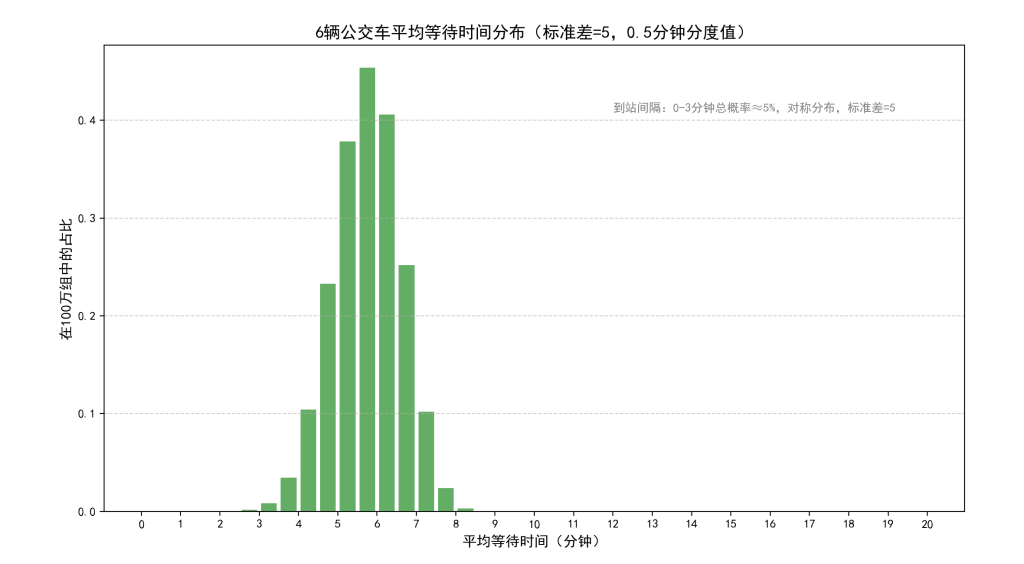
可以观察到，在正常情况下4.5-5分钟以及5-5.5分钟的概率分别都低于6-6.5分钟和5.5-6分钟，符合公交车悖论的内容，并且平均等待时间大概在6分钟左右（目测）。

3.拓展内容

毕导在视频里提到：你的朋友大概率比你有更多朋友，于是我写了个CPP，专门计算你的朋友到底有多少个朋友（当然这个代码只适用于我们班男生的学号，请自行调整），代码如下（不知道对不对）：

#include <bits/stdc++.h>
using namespace std;
int g[45][45],num[45];
int y,n,d;
double getavr(int a)
{
	double avr=0;
	for (int i=1;i<=num[a];i++)
	{
		avr+=num[g[a][i]];
	}
	avr/=num[a];
	return avr;
} 
int main()
{
	int a;
	while (a!=0)
	{
		cin>>a;
		if (a==0) break;
		else
		{
			int b=1;
			while (b!=0)
			{
				cin>>b;
				num[a]++;
				g[a][num[a]]=b;
			}
			num[a]--;
		}
	}
	cout<<"学号"<<'\t'<<"朋友的平均朋友数"<<'\t'<<"是否比本人朋友数多"<<endl;
	for (int i=18;i<=43;i++)
	{
		if (i==19||i==22||i==39||i==40||i==43) continue;
		cout<<i<<'\t'<<'\t'<<getavr(i)<<'\t'<<'\t'<<'\t';
		if (getavr(i)>num[i])
		{
			cout<<"是"<<endl;
			y++;
		}
		else if (getavr(i)==num[i])
		{
			cout<<"一样多"<<endl;
			d++;
		}
		else
		{
			cout<<"否"<<endl;
			n++;
		}
	}
	cout<<y<<" "<<n<<" "<<d;
	return 0;
}